Median adalah Nilai Tengah Data, Begini Cara Mudah Mencarinya
KOMPAS.com - Pernahkah kamu menghitung nilai tengah dari sekumpulan angka? Jika ya, maka kamu sudah berkenalan dengan median. Tapi, apa yang dimaksud dengan median sebenarnya?
Median adalah nilai tengah dari sekumpulan data yang telah diurutkan dari yang terkecil hingga terbesar. Jika jumlah data ganjil, median adalah nilai di posisi tengah. Jika jumlah data genap, median diperoleh dari rata-rata dua nilai tengah.
Median mencerminkan posisi tengah data, sehingga tidak dipengaruhi oleh nilai ekstrem (terlalu besar atau kecil).
Untuk lebih memehami median, yuk kita simak penjelasan di bawah ini!
Baca juga: Menentukan Rata-rata, Median, dan Modus dari Data
Pengertian median
Menurut Setiawan dan Pepen Permana dalam Pengantar Statistik (2008), median adalah nilai tengah dari data yang telah diurutkan dari yang paling kecil ke paling besar (atau sebaliknya).
Dalam statistik, definisi median menjelaskan bahwa angka ini membagi data menjadi dua bagian yang sama besar. Artinya, setengah data berada di bawah median dan setengah lainnya di atas.
Median adalah nilai tengah dari gugusan data yang telah disusun berurutan.
Rina Candra Noor Santi dan Sri Erniyati dalam Implementasi Statistik dengan Database MySQL (2015), menambahkan bahwa median merupakan rata-rata dari sisi kedudukannya dalam data, bukan dari jumlah nilainya.
Baca juga: Mengenal Kelebihan dan Kekurangan Median atau Nilai Tengah
Cara mencari median
Terdapat dua cara utama dalam menghitung median, tergantung pada jenis data yang kita miliki: apakah itu data tunggal atau data kelompok.
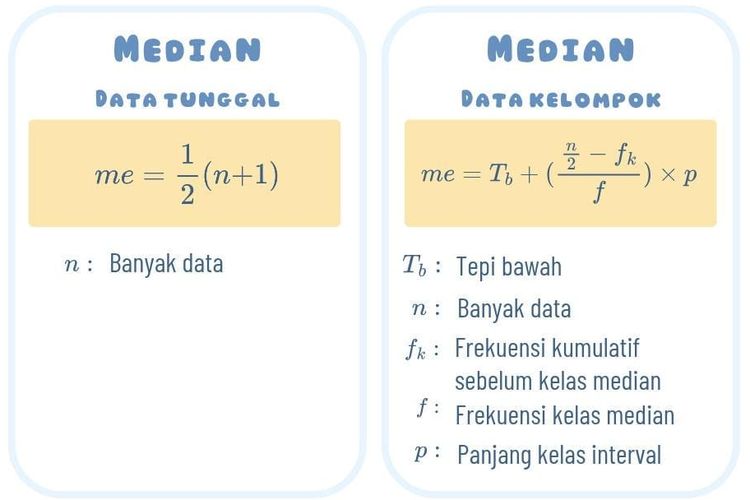
1. Median data tunggal
Untuk data tunggal (yaitu data yang belum dikelompokkan), cara mencari median cukup sederhana. Kamu hanya perlu mengurutkan datanya, lalu mencari posisi tengah dengan menggunakan rumus median berikut:
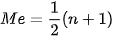
Di mana n adalah jumlah data yang tersedia.
Contoh: Jika kamu memiliki 9 data, maka posisi median adalah di urutan ke-5. Nilai pada posisi itulah yang menjadi mediannya.
Baca juga: Pengertian dan Rumus Median Data Tunggal
2. Median data kelompok
Untuk data yang telah dikelompokkan ke dalam tabel distribusi frekuensi, media data kelompok atau median data berkelompok harus dihitung menggunakan rumus khusus. Berikut adalah rumus median untuk data berkelompok:
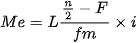
Dengan:
- L: tepi bawah kelas median
- n: jumlah seluruh data
- F: frekuensi kumulatif sebelum kelas median
- fm: frekuensi dari kelas median
- i: panjang interval kelas
Rumus ini digunakan saat data terlalu banyak untuk dianalisis secara individual, sehingga dibagi menjadi kelas-kelas.
Baca juga: Rumus Median Data Berkelompok beserta Contoh Soalnya
Median sangat berguna untuk mengetahui pusat data, terutama ketika data memiliki nilai-nilai ekstrim yang bisa "mengganggu" perhitungan rata-rata.
Misalnya, dalam pengukuran pendapatan penduduk suatu wilayah, penggunaan median sering kali lebih representatif dibanding rata-rata biasa.
Contoh soal menghitung median
Contoh soal 1: menghitung median data tunggal
Ada 10 Sekolah Menengah Pertama di suatu kota. Banyaknya kelas di masingmasing sekolah ditunjukkan di bawah ini. Hitunglah mediannya!
6, 12, 9, 7, 6, 18, 4, 9, 6, 12
Jawaban:
Langkah-langkah mencari median data tunggal:
1. Urutkan data dari yang terkecil ke yang terbesar:
4, 6, 6, 6, 7, 9, 9, 12, 12, 18
2. Hitung jumlah data:
n = 10 (data genap)
3. Cari posisi median dengan rumus posisi ke-
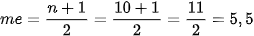
4. Ambil nilai pada posisi 5,5 atau ke-5 dan ke-6 dalam data yang sudah diurutkan:
Nilai ke-5 = 7
Nilai ke-6 = 9
5. Hitung rata-rata dari kedua nilai tersebut:
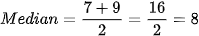
Jadi, median dari data tersebut adalah 8.
Baca juga: Cara Menghitung Mean, Median, Modus pada Data Nilai Matematika
Contoh soal 2: median data berkelompok
Berikut adalah data jumlah buku yang dibaca siswa selama sebulan:
Jumlah Buku
| Jumlah Buku | Frekuensi |
| 1-3 | 4 |
| 4-6 | 6 |
| 7-9 | 10 |
| 10-12 | 5 |
| 13-15 | 3 |
Tentukan median dari data di atas!
Jawaban:
1. Hitung jumlah total frekuensi (n):
n = 4 + 6 + 10 + 5 + 3 = 28
2. Tentukan n/2:
n/2 = 28/2 = 14
(Kita cari posisi data ke-14 → ini menentukan kelas median)
3. Buat tabel frekuensi kumulatif:
| Jumlah Buku | Frekuensi | Frekuensi kumulatif |
| 1-3 | 4 | 4 |
| 4-6 | 6 | 10 |
| 7-9 | 10 | 20 |
| 10-12 | 5 | 25 |
| 13-15 | 3 | 28 |
Baca juga: Rumus Frekuensi Gelombang
4. Identifikasi elemen rumus:
- L = 6.5 → tepi bawah kelas 7–9
- F = 10 → frek. kumulatif sebelum kelas median
- fm = 10 → frekuensi kelas median
- i = 3 → panjang interval (9 – 6 = 3)
5. Gunakan rumus median data berkelompok:
Me = L + [(n/2 – F) / fm] × i
Me = 6,5 + [(14 – 10) / 10] × 3
Me = 6,5 + [4 / 10] × 3
Me = 6,5 + 0,4 × 3
Me = 6,5 + 1,2
Me = 7,7
Baca juga: Pengertian Kisaran Nilai Peluang dan Frekuensi Relatif
Sehingga, median adalah alat penting dalam analisis data. Baik dalam bentuk data tunggal maupun kelompok, cara mencari median dapat disesuaikan dengan rumus yang tepat.
Jadi, jika kamu sedang mengolah data dan bertanya-tanya apa yang dimaksud dengan median, ingatlah bahwa median adalah nilai tengah yang adil dan tidak terpengaruh oleh angka-angka ekstrem, dan memberikan gambaran yang seimbang dari distribusi data.
Ingin mencoba? Urutkan datamu dan temukan median untuk melihat bagaimana si “penengah” ini bisa memberi pandangan baru terhadap datamu!
Simak breaking news dan berita pilihan kami langsung di ponselmu. Pilih saluran andalanmu akses berita 优游国际.com WhatsApp Channel : . Pastikan kamu sudah install aplikasi WhatsApp ya.